Spheroids and Ellipsoids
For the full details, click here.
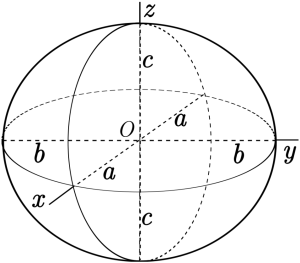
The standard equation of an ellipsoid in the coordinate frame depicted above is
|
+ |
|
+ |
|
= 1 |
The points (a,0,0), (0,b,0) and (0,0,c) lie on the surface and the line segments from the origin to these points are called the semi-principal axes of length a, b, c. There are four distinct cases:
- a > b > c : scalene ellipsoid
- a = b > c : oblate ellipsoid of revolution (oblate spheroid, aka "bun")
- a = b < c : prolate ellipsoid of revolution (prolate spheroid, aka "cigar")
- a = b = c : circle of revolution (sphere)
The oblate and prolate spheroids are symmetrical around the z-axis, and can be respectively likened to spheres that have been flattened or elongated along the +ve and –ve z-axes.
More precisely, the oblate or prolate ellipsoids can be generated by rotating the (x,z) ellipse through 180° around the z-axis, after first choosing c<a in the oblate case, or c>a in the prolate case. In both cases, b becomes necessarily equal to a.
In the context of domes, of course, we're really only interested in the upper halves (hemispheres or semi-ellipsoids) of these shapes.