The Catenary Equation
The book I'm about to reference is the most magical and fascinating accomplishment. Small wonder that its author is the daughter of Dr Jacob Bronowski, possibly the most erudite, influential and beloved of all the major intellectuals in British public life a generation or two ago. Prof Jardine's book has much to tell us in numerous places about Hooke, Wren, St Paul's Cathedral and the catenary curve. Here is one extract.
pp 332-3, Ingenious Pursuits: Building the Scientific Revolution, Lisa Jardine1, 2, Little Brown & Company (UK), London 1999
But what did he really come up with?
- Huyghens' solution was closely scrutinised in a recent review
Christiaan Huygens and the Problem of the Hanging Chain, John Bukowski, The College Mathematics Journal, Vol 39, No 1, Jan 2008 jcsites.juniata.edu/faculty/bukowski/hm/cmj002-011.pdf or click here.
but you will search it in vain for an explicitly-stated algebraic solution.
- Leibniz' solution is reproduced in a recent reprint
FIDELIO Magazine, Vol. X No.1, Spring 2001 schillerinstitute.org/fid_97-01/011_catenary.html or click here.
but once again there is no sign of an explicitly-stated algebraic solution.
I can't find any detailed account of the solution provided by Johann (aka Jean) Bernoulli, the other successful contestant, but it isn't likely to have been explicit either. There is absolutely no doubt that all three of these three great mathematicians had correctly and unambiguously characterised the curve, but they had done so in non-algebraic terminology.
Indeed, the vital concept that they lacked, the natural exponential function exp(x) = ex was only first defined and investigated some years later, by the self-same Johann Bernoulli, who published his findings in the best-selling Principia calculi exponentialium seu percurrentium in 1697.
I'm beginning to suspect that my audience is getting a bit restive, shuffling its feet and looking surreptitiously at its wristwatch. Indeed one or two of the rowdier elements at the back are starting a slow handclap and a chant of "Why are we waiting?". There could well be a rush for the exits if this elusive formula isn't revealed pretty soon, and so you may like to click here and now for a very clear and authoritative derivation presented in a deservedly popular textbook first published over a century ago.
But as Oscar W remarked about the cigarette, it is exquisite, and it leaves one unsatisfied. By this I mean that that the derivation has an economy and subtlety that practically brings tears to the eye, but it demands more of the reader than most people would feel comfortable with these days. It also leaves one completely in the dark as to how the formula could be used in practice, as there is no explanation as to how the parameters involved can be deduced from practical realities. For both these reasons, and also because I love explaining things, a more detailed treatment is now presented. Or you could rush for the exit.
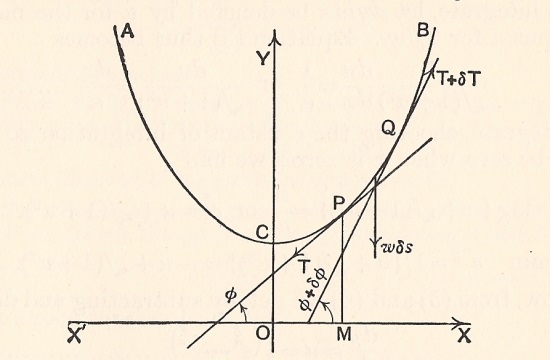
Curve ACB is the catenary of course, A and B being the suspension points. The chain is assumed to be uniform, with a linear density (ie weight per unit length) of w. PQ represents a typical small section of the chain, of length δs and mass w δs.
The conditions for static equilibrium of this small section were discussed earlier, and they can be represented algebraically as follows
For vertical equilibrium | ||||||||||||||||||||
| • [Eqn 1a] | (T + δT) sin(ϕ + δϕ) – T sinϕ = w δs | |||||||||||||||||||
and for horizontal equilibrium | ||||||||||||||||||||
| • [Eqn 1b] | (T + δT) cos(ϕ + δϕ) – T cosϕ = 0 | |||||||||||||||||||
as tension T + δT acts (at angle ϕ + δϕ) tangentially upwards at Q and tension T acts (at angle ϕ) tangentially downwards at P. Seemples – that's the physics over, the rest is purely calculus and is slightly tougher (but help is available via the activated equation numbers). We notice that the LHS's of these equations are identically the increments of T sinφ and T cosφ respectively, and so can be written as | ||||||||||||||||||||
| • [Eqn 2a] | δ(T sinϕ) = w δs | |||||||||||||||||||
| • [Eqn 2b] | δ(T cosϕ) = 0 | |||||||||||||||||||
[Eqn 2b] implies that T cosϕ is unvarying, as its increment is zero, and so | ||||||||||||||||||||
| • [Eqn 3] | T cosϕ = T0 | |||||||||||||||||||
where T0 is a constant, indicating that the horizontal component of tension is numerically the same along the entire length of the catenary. [Eqn 2a] implies that, in the infinitesimal limit where increments become differentials, | ||||||||||||||||||||
| • [Eqn 4] |
| |||||||||||||||||||
Now for some legerdemain: as (by definition) sinϕ = cosϕ • tanϕ we can use [Eqn 3] to give | ||||||||||||||||||||
| • [Eqn 5a] | sinϕ = (T0/T) tanϕ | |||||||||||||||||||
| • [Eqn 5b] | T sinϕ = T0 tanϕ | |||||||||||||||||||
And then substitute this into [Eqn 4] to give | ||||||||||||||||||||
| • [Eqn 6a] |
| |||||||||||||||||||
Then by use of the chain rule for changing the independent variable in the derivative from s to x | ||||||||||||||||||||
| • [Eqn 6b] |
| |||||||||||||||||||
But tanϕ has an independent significance: as ϕ is the tangential angle, tanϕ is, by very definition, identically equal to the derivative of y with respect to x | ||||||||||||||||||||
| • [Eqn 7a] |
| |||||||||||||||||||
| • [Eqn 7b] |
| |||||||||||||||||||
and ds itself can also be expressed in terms of x and y, using Pythagoras' Theorem | ||||||||||||||||||||
| (ds)2 = (dx)2 + (dy)2 | ||||||||||||||||||||
which on division throughout by (ds)2 becomes | ||||||||||||||||||||
| • [Eqn 8a] |
| |||||||||||||||||||
| • [Eqn 8b] |
| |||||||||||||||||||
And now putting together [Eqn 6a], [Eqn 6b], [Eqn 7b] and [Eqn 8b] we get | ||||||||||||||||||||
| • [Eqn 9] |
| |||||||||||||||||||
This second-order second-degree differential equation looks pretty formidable, but is actually a poodle in bulldog's clothing. Let's start with a couple of notational simplifications | ||||||||||||||||||||
| • [Eqn 10a] |
| |||||||||||||||||||
| • [Eqn 10b] |
| |||||||||||||||||||
whereupon [Eqn 9] dramatically simplifies to | ||||||||||||||||||||
| ||||||||||||||||||||
Then, on separating the variables, | ||||||||||||||||||||
| • [Eqn 11a] |
| |||||||||||||||||||
followed by integration from (x=0, u=0, ie the bottom of the curve) to (x,u) | ||||||||||||||||||||
| • [Eqn 11b] |
| |||||||||||||||||||
we get | ||||||||||||||||||||
| • [Eqn 11c] |
| |||||||||||||||||||
Exponentiating both sides, this becomes | ||||||||||||||||||||
| • [Eqn 11d] | ex/a = u + √(1+u2) | |||||||||||||||||||
And, furthermore, | ||||||||||||||||||||
| • [Eqn 11e] | e–x/a = –u + √(1+u2) | |||||||||||||||||||
Subtracting [Eqn 11e] from [Eqn 11d] and dividing by 2 | ||||||||||||||||||||
| • [Eqn 11f] | u = ½ (ex/a + e–x/a) | |||||||||||||||||||
These ingenious manipulations have simply oven-readied the first-order differential equation for a straightforward further integration, recalling the definition of u from [Eqn 10a] | ||||||||||||||||||||
| • [Eqn 12a] |
| |||||||||||||||||||
Separating the variables and integrating from (x=0, y=a, ie the bottom of the curve) to (x,y) | ||||||||||||||||||||
| • [Eqn 12b] |
| |||||||||||||||||||
we finally obtain The Formula! | ||||||||||||||||||||
| • [Eqn 12c] | y = ½ a (ex/a + e–x/a) | |||||||||||||||||||
This is as far as we were taken by Prof Gibson in the here and now link, but we must now prepare to go further, to relate it to practical realities. The first step is to bring in the hyperbolic sine function sinh( ) and the hyperbolic cosine function cosh( ) in terms of which The Formula and its derivative take a neater form | ||||||||||||||||||||
| • [Eqn 13a] | y = a cosh(x/a) | |||||||||||||||||||
| • [Eqn 13b] |
| |||||||||||||||||||
The second step is to identify the dimensions in terms of which the catenary can be uniquely characterised, and then to relate the algebraic parameters to them. There are three such dimensions
Length From [Eqn 8b] we can set | ||||||||||||||||||||
| • [Eqn 14a] | ds = √ {1 + (dy/dx)2} • dx | |||||||||||||||||||
And then from [Eqn 13b] | ||||||||||||||||||||
| • [Eqn 14b] | ds = √ {1 + sinh(x/a)2} • dx | |||||||||||||||||||
which becomes | ||||||||||||||||||||
| • [Eqn 14c] | ds = cosh(x/a) dx | |||||||||||||||||||
Integrating from (0,0) to (ℓ, d) | ||||||||||||||||||||
| • [Eqn 14d] |
| |||||||||||||||||||
we get | ||||||||||||||||||||
| • [Eqn 14e] | ℓ = a sinh(d/a) | |||||||||||||||||||
Interestingly, this is equivalent to | ||||||||||||||||||||
| • [Eqn 14f] | ℓ = a tanϕmax | |||||||||||||||||||
where ϕmax is the value of ϕ at the point of suspension B. (Even more esoteric is the more general relation s = a tanϕ, which is the most generalised equation of the catenary, of the kind that Whewell categorised as "intrinsic".) But cutting to the chase, as my erstwhile boss used to quote from his book of MBA maxims and mantras, [Eqn 14e] enables the parameter a to be evaluated from a knowledge of the half-length ℓ and semi-span d of the catenary. The equation is implicit rather than explicit, and would have to be iterated to self-consistency. Sag The sag is clearly equal to the ordinate of the catenary at the transect AB less the ordinate of the catenary at the bottom C. From [Eqn 13a] this amounts to | ||||||||||||||||||||
| • [Eqn 15] | h = a cosh(d/a) – a | |||||||||||||||||||
[Eqn 15] enables the parameter a to be evaluated from a knowledge of the sag h and semi-span d of the catenary. Once again, the equation is implicit rather than explicit, and would have to be iterated to self-consistency. Span Both methodologies so far have needed the span as input, but is it possible to calculate the parameter a using just the sag h and half-length ℓ, without using the span? I think it is. | ||||||||||||||||||||
| • [Eqn 14e] says ℓ = a sinh(d/a); [Eqn 15] says h + a = a cosh(d/a) | ||||||||||||||||||||
But these are closely linked through the hyperbolic functional identity | ||||||||||||||||||||
| • [Eqn 16] | cosh2( ) – sinh2( ) = 1 | |||||||||||||||||||
So we get | ||||||||||||||||||||
| • [Eqn 17a] | {(h + a)/a}2 – (ℓ/a)2 = 1 | |||||||||||||||||||
which simplifies to | ||||||||||||||||||||
| • [Eqn 17b] | a = (ℓ2 – h2) / 2h | |||||||||||||||||||
This unexpectedly simple relationship is a really happy discovery. It's an explicit equation and can be evaluated immediately. DG. | ||||||||||||||||||||